Time series clustering

What is clustering?

Clustering is an unsupervised learning task that partitions a set of unlabeled data objects into homogeneous groups or clusters. As we are in the unsupervised setting, we do not possess advanced knowledge of the definitions or classifications of the groups. The objective of such a task is to form clusters wherein individuals have maximum similarity with other individuals within the group, and minimum similarity with individuals in other groups. This approach can be used for data mining, identifying structures in unlabeled data sets, summarizing data, or as a pre-processing step in a more complex modeling system.

In which context?

In recent years, the increasing power of data storage systems and processors has enabled real-world applications to store and keep data for long timescales. The emergence of various big data concepts including machine learning and AI has allowed us to address issues associated with exponentially larger data sets. Considerable changes in data modeling have been made and the field of time series data is no exception. Time series clustering benefitted from improvements in recent years to cope with this avalanche of data and the increasing number of use cases thereby preserving its reputation as a helpful data-mining tool for extracting useful patterns and knowledge from big datasets.

Time series clustering ?

Data for many applications is stored in time-series format, for example : weather data, sales data, biomedical measurements like blood pressure and electrocardiogram, stock prices, biometrics data etc. Accordingly, different works are found in a variety of domains such as energy, finance , bioinformatics or biology. Many projects relevant to analyzing time-series have been performed in various areas for different purposes such as: subsequence matching, anomaly detection, motif discovery, indexing, visualization, segmentation, identifying patterns, trend analysis, summarization, and forecasting.

What are the main challenges?

Clustering time-series in the context of large datasets is a difficult problem, for main two reasons. Firstly, time-series data are often of high dimension, which makes handling these data slow and difficult for many clustering algorithms. The second challenge addresses the similarity measures used to make the clusters.

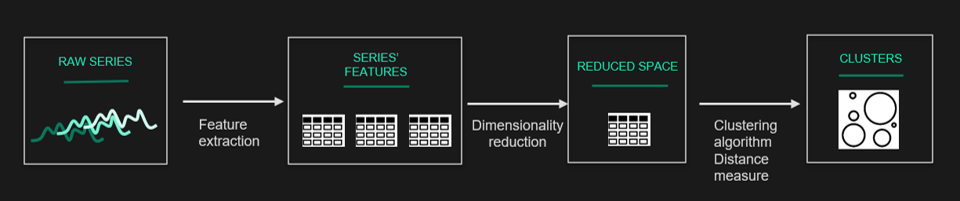
Four components of time-series clustering are identified in the literature: dimensionality reduction or representation method, distance measurement, clustering algorithm, and evaluation. In the rest of this article, we will provide an overview of these components.

From the raw series (temporal-proximity based clustering)

Classical clustering methods can be applied directly to the initial series.

But beware, in this case, the choice of the distance/similarity measure must be carefully considered before the application of the algorithm. The selection involves determining what is meant by “similarity” between individual time-series and can vary depending on the particularities of the data.

In practice, we rarely use the raw series directly. Instead, a preliminary processing is performed to yield a simplified version of the series. We will see why this is useful and sometimes necessary in the next section.

From a simplified representation of the series (representation-based clustering)

Simplified representation with quick reduction of the problem dimension

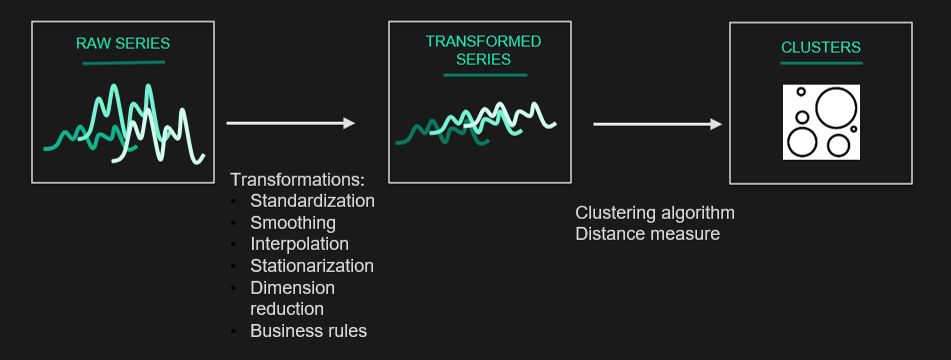
The raw data can be processed before clustering by applying transformations: standardization, smoothing, interpolation, stationarization etc. These processes can remove noise and unwanted trends from the data and we can apply clustering algorithms to the resulting series.

The figure illustrates the impact of data preparation:

The similarity and distance measures discussed later in the article can then be applied, but the computation time for some of these can be too long for large databases. We must then rely on dimensional reduction techniques.

Simplified representation with complex reduction of the problem dimension

In this section we discuss ideas of dimensional reduction, which in this context refers to either reduction of the number of points in time-series or the elimination of components in series that are not relevant to the given study. In some cases it is desirable to reduce the size of the initial series. This reduction must occur such that the reduced series retains the main characteristics of the initial series (with a transformation that preserves similarities and distances). So we look for a space of reduced dimensionality that allows to extract the main characteristics of the series and to reduce their size.

The reason that dimensionality reduction is important to the clustering of time-series is firstly that it reduces memory requirements. Secondly, distance calculation with raw data is computationally expensive, and dimensionality reduction significantly speeds up clustering. There is a trade-off between speed and quality.

A simple and well known example is to use the fast Fourier transform. Any “nice” mathematical function of time can be described by a combination of sine and cosine functions of frequency:

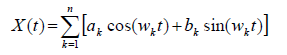
In this decomposition into sines and cosines, the coefficients a and b represent the contribution of the frequency ω to the series X. Lower frequencies will reflect the trend and cycle of the series, for example the seasonal frequencies. We can thus obtain a simplified representation of the series by retaining only “the most important” Fourier coefficients. The table below shows an example of reduction of the dimension of a time series by Fourier transform.

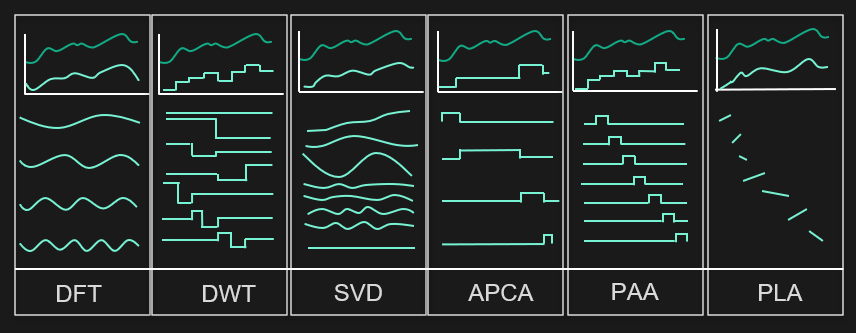
The same principle can be applied to many other transformations:

• Discrete Fourier Transform : DFT
• Discrete Wavelet Transform : DWT
• Singular Value Decomposition via PCA : SVD
• La SSA (singular spectrum analysis) (see time series modeling tutorial)
• Piecewise Aggregate Approximation : PAA
• Adaptive Piecewise Constant Approximation : APCA
• Piecewise Linear Approximation : PLA
• Symbolic Approximation SAX
• Auto-encoder

Here are some examples of such transformations:

Simplified representation with business rules

Another possible simplification of the data is to apply “business rules”. Indeed, depending on the use case, it is possible to reduce the dimension of the problem without using statistical methods. Consider for example a time series representing electricity consumption over a one year period with measurements taken at 30-minute intervals. It is quite possible, depending on the objective, to aggregate the series (at hourly intervals for example), or to condense repeating patterns and create shorter series (averages of winter and summer weeks), etc. Depending on the case, we can change our starting dataset and reduce the size of the problem.

Model-based clustering

Another idea is to model time series to capture and summarize their dynamics. Two series will then be similar if the fitted models are similar. Several ideas have been exploited in the literature:

• An autoregressive model, or even ARIMA, can be fitted to the series. These models are then compared using a particular metric.
• Hidden Markov models.

However, in practice, it is shown that usually model-based approaches have scalability problems, and can lead to performance reductions when the clusters are close to each other. These methods are therefore rarely used.

From feature extraction (characteristic-based clustering)

Here we push the model-based clustering logic further: we use several measures that allow us to qualify the time series (trend, seasonality, autocorrelation, non-linearity, skewness, kurtosis, etc.). These are features that can be extracted to describe each series.

We then go from a raw series to the features of the series. We can create hundreds of features for each series. It can therefore be interesting to set up a selection process of the relevant variables and/or to apply a dimension reduction algorithm.

Finally, once again, we can apply the choice of distance measure/algorithm that we want depending on the implementation constraints.

In time series clustering similarity/dissimilarity measures play an important role, and have a major impact on the clustering results. However, choosing the right measure is not an obvious task. Some similarity measures are proposed based on specific transformed time-series, and some of them work regardless of the applied transformation, or are compatible with raw time series.

Normally, when performing a “classical” clustering, the distances between individuals are “match based”,that is comparison is fixed by a certain feature. However, for time series clustering distance can be calculated approximately. This makes it possible to calculate the distance between series with irregular sampling intervals and length. It is often not necessary to look for very exotic measures, there are popular and efficient distance measures such as The Hausdorff distance (DH), modified Hausdorff (MODH), HMM-based distance, Dynamic Time Warping (DTW), Euclidean distance, Euclidean distance in a PCA subspace, and Longest Common Sub-Sequence (LCSS)

The choice of distance measure obviously depends on the objectives of the use case, on the time series characteristics (such as length), and on the representation method. Research shows that common time series properties such as noise, amplitude scaling, offset translation, longitudinal scaling, linear drift, discontinuities and temporal drift can introduce challenges to the selection and interpretation of distance measures..

A wide range of measures

Hundreds of distances have been proposed to classify data, of which the Euclidean distance is the most popular. However, when it comes to clustering time series, using the Euclidean distance, or any other Minkowski metric, on raw data can lead to unintuitive results. In particular, this distance is very sensitive to scale effects and to atypical or missing data points. The Euclidean distance does not allow temporal shifts to be taken into account. Indeed, very similar signals can be shifted in time and would not be measured as “close” in the standard Euclidean distance. To solve this problem there are adapted metrics such as the DTW (Dynamic Time Warping) distance.

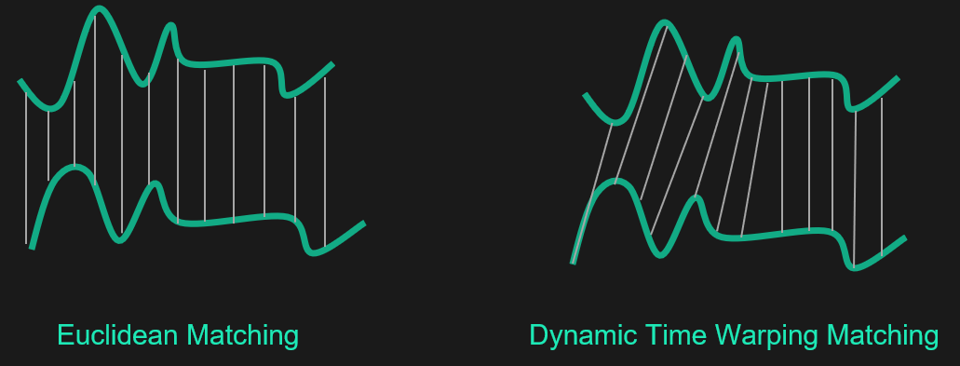
This distance considers a non-linear elastic time and consequently explains relative temporal shifts of two series by deforming the time axis. Intuitively, this means that this distance does not compare only points with matching timestamps. Thus, the Euclidean distance only takes into account simultaneous events, whereas the DTW distance takes into account out of phase events. Of course it is not a magic measure that works in all cases. There is no metric or clustering algorithm that can be said to outperform all others. It all depends on the application context, so it’s up to you to experiment with different alternatives, and choose the best one.

Depending on the measure selected, the resulting clusters can be “closer” in either time or shape. These differences in cluster parameters can also be impacted by the data treatment methods discussed above. Depending on the clustering objective and the length of time series, the four methods of treating data mentioned above can be tested. Clustering can either be applied to the raw time series, to a simplified representation of the series, to time series models, or to features extracted. Measures can then be applied impacting the temporal or geometric similarity of the clusters. Some examples from literature are:

• Temporal proximity based similarity measure is to find the similar time series in time and shape like Euclidean, DTW, LCSS, etc.
• Compression based similarity measure : suitable for short and long time series such as CDM, Autocorrelation, Short time- series distance, Pearson’s correlation coefficient and related distances, Cepstrum, Piecewise normalization and Cosine wavelets.
• Features based similarity measure : proper for long time series such as statistics, coefficients, etc.
• Model based similarity measure such as ARMA

Discussion on distance measures

There are many distance measures proposed by researchers and choosing an adequately adapted distance measure is controversial in the time series clustering domain. However, the following conclusions can be made :

• A trade-off between speed and accuracy should be considered.
• A big challenge is the issue of incompatibility of a given distance metric with the representation method. For example, the frequency-domain is a useful approach to dimensional reduction but it is difficult to find good similarity measures and to produce value-based differences in this space for clustering.
• Euclidean distance and DTW are the most common similarity measures in time-series clustering. Research has shown that, in terms of time series classification accuracy, the Euclidean distance is surprisingly competitive, however, DTW also has strengths that cannot be denied.

Generally clustering can be broadly classified into five groups: Hierarchical, Partitioning, Model-based, Density-based and Multi-step or hybrid clustering algorithms. In the following, the application of each group to time-series clustering is discussed.

Hierarchical clustering

Hierarchical cluster analysis or HCA is an unsupervised clustering algorithm, it is one of the most popular and easily understood clustering techniques. This class of clustering has two algorithm types:

1. Agglomerative hierarchical clustering : considers each item as a cluster, and then gradually merges the clusters (bottom-up)
2. Divisive hierarchical clustering: starts with all objects as a single cluster and then splits the cluster to reach the clusters with one object (top-down).

In general, hierarchical algorithms are weak in terms of quality of performance because they cannot adjust the clusters after either splitting a cluster in a divisive method (type 2), or after merging clusters in an agglomerative method (type 1). As a result, usually hierarchical clustering algorithms are combined with another algorithm as a hybrid clustering approach to remedy this issue.

Without going into too much detail about the algorithm, it generates a pair-wise distance matrix of time-series. In order to generate this matrix, and specifically to calculate the distances/similarities between the series, it is necessary to choose a distance/similarity measure. The choice will obviously impact the algorithm results. The distance matrix also enables visualization of the Hierarchical clustering process (for example dendrograms), offering power when it comes to interpretability.

Additionally, one of the great strengths of this algorithm is the fact that it does not need the number of clusters to be returned as an input parameter. This is an outstanding feature because it can be very difficult to find this parameter and is sometimes necessary for algorithms as we will see in the following.

Moreover, hierarchical clustering algorithms have the capacity to cluster time-series of different lengths. It is possible to cluster time-series of varying lengths using this algorithm if an appropriate elastic distance measure such as Dynamic Time Warping (DTW) or Longest Common Sub-sequence (LCSS) is used to compute the dissimilarity/similarity of time-series. However, hierarchical clustering is effectively incapable of dealing with large time-series due to its quadratic computational complexity and this poor scalability thus leads to its restricted use on small datasets.

Apart from the choice of algorithm and distance measure, it is necessary to choose the aggregation criterion. From several iterations of a hierarchical algorithm, we will have to consider the distance between groups of individual time-series and the following question will arise: how to calculate the distance in the presence of groups? Different possibilities exist.

First of all, three criteria that work regardless of the distance/dissimilarity measure are (among many others):

• The minimum linkage criterion (or single linkage), which is based on the two closest time-series;
• The maximum linkage criterion (complete linkage), which is based on the two most distant elements;
• The average linkage criterion, which will use the average of the distances between the elements of each class to perform the groupings.

In the framework of Euclidean distance, other criteria can be used. The most commonly used is Ward’s criterion, which is based on the increase of inertia. Without going into detail, this criterion amounts to aggregating two classes such that the increase of the intra-class inertia is as small as possible, so that the classes remain as homogeneous as possible.

Depending on the criterion chosen, we can end up with trees having very different shapes. In the end, it is important to remember that there is no single best method, just as there is no single clustering method. It is recommended to test several approaches and analyze the results.

Partitioning clustering

The objective of non-hierarchical clustering is the same as that of hierarchical clustering, but in this case, the number of clusters has to be pre-assigned. For a given distance measure and for a known number of classes k, it is easy to imagine a simple and optimal classification solution: enumerate all conceivable clustering possibilities and keep the best one. However, this solution is not applicable in practice, because the number of possible combinations of groupings quickly becomes enormous. Approximate solutions can be obtained thanks to heuristics and several algorithms of this kind exist. Their fundamental principle is based on the method of moving centers.

The working principle of moving centers is the minimization of the total distance (typically Euclidian distance) between all objects in a cluster from the cluster center.

The algorithm does not necessarily lead to a global optimum: the final result depends on the initial centers. In practice, we run the algorithm several times (with different initial centers). Then, either we keep the best solution, or we look for stable groupings to identify the individual series belonging to the same partitions.

The best-known algorithms exploiting mobile centers are :

• The K-means method
• The dynamic clustering methods
• The K-medoids methods

In these clustering algorithms, the number of clusters, k, has to be pre-assigned, which is a very complicated task for clustering non-time-series data. It is even more challenging with time-series data because the datasets are very large and diagnostic checks for determining the number of clusters are not easy.

However, these algorithms are very fast compared to hierarchical clustering and this makes them very suitable for time-series clustering, as has been shown in many works. You can build your clusters in a ‘hard’ or ‘soft’ manner which means that either an object is assigned to a cluster (hard) or an object is assigned a probability of being in a cluster (soft).

Model-based clustering

Model-based clustering assumes that the data was generated by a model and tries to recover the original model from the data. In the literature there are quite few research publications that demonstrate the value of these methods. Most of the time they build their clustering with polynomial models, Gaussian mixed models, ARIMA, Markov chain, Hidden Markov or Neural Network approaches. In general, model-based clustering has two drawbacks: first it has a slow processing time on large datasets. Second, and more importantly, model-based clustering requires input parameters and assumptions which may not be correct for the use case and could result in inaccurate clusters.

This method will not be discussed further as it is almost never used in practice.

Density-based clustering

Density-Based Clustering refers to unsupervised learning methods that identify distinctive groups/clusters in the data, based on the idea that a cluster in a data space is a contiguous region of high point density, separated from other such clusters by contiguous regions of low point density. One of the most well-known algorithms based on this density-based concept is DBSCAN. However, a literature review reveals that density-based clustering has not been broadly applied to clustering time-series data due to the high complexity of this task.

Hybrid approach (multi-step clustering)

In the previous sections, we presented the clustering algorithms individually. However, in practice, it can be useful to use them together. By combining approaches, one can exploit the main advantages of the different methods, namely :

• The ability to analyze a large number of individual time-series, which is the strong point of non-hierarchical methods (for a certain number of observations it becomes difficult to apply hierarchical methods directly);
• The choice of an optimal number of classes, made possible by hierarchical classification.

In practice, as soon as the data set becomes large, it is recommended to implement a hybrid approach to have the best trade-off between performance and speed of execution.

Correctly evaluating the performance of a clustering procedure is always an open problem, in general and specifically for time series clustering. In unsupervised problems, we do not have labels to establish performance metrics. The definition of a “good” clustering depends on the problem and is often subjective. The number of clusters, the cluster size, the definition for outliers, and the definition of similarity among time-series in a problem are all the concepts which depend on the task at hand.

The evaluation of time series clustering should follow recommendations from some disciplines: :

• Implementation bias must be avoided by careful design of the experiments,
• New methods of similarity measures should be compared with simple and stable metrics such as Euclidean distance.

The results can be evaluated by using various measures. Visualization and scalar measurements are the major evaluation techniques for clustering quality, which is also known as clustering validity.

Typical objective functions in clustering formalize the goal of attaining high intra-cluster similarity (objects within a cluster are similar) and low inter-cluster similarity (objects from different clusters and dissimilar). Internal validation compares solutions based on the goodness of fit between each clustering and the data. Internal validity indices evaluate clustering results by using only features and information inherent in a dataset. They are usually used in the case that true solutions (ground truth) are unknown.

Clusters can be characterized using for example common statistical tools such as means, standard deviations, min/max, etc. Also there are many internal indices such as Sum of Squared Error, Silhouette index, Davies-Bouldin, Calinski-Harabasz, Dunn index, R-squared index, Hubert-Levin (C-index), Krzanowski-Lai index, Hartigan index, Root-Mean-Square Standard Deviation (RMSSTD) index, Semi-Partial R-squared (SPR) index, Distance between two clusters (CD) index, Weighted inter-intra index, Homogeneity index, and Separation index. Sum of Squared Error (SSE) is an objective function that describes the coherence of a given cluster; “better” clusters are expected to give lower SSE values. For evaluation of clusters in terms of accuracy, the Sum of Squared Error (SSE) is commonly used. For each time-series, the error is the distance to the nearest cluster.

However, in the context of clustering, the business perspective is often a factor when considering clustering performance. There may be impossible results that we don’t want, particular expectations, a number of clusters to respect etc.

The intrinsic characteristics of the data, the time series, make the clustering exercise a real challenge. Indeed, it is difficult to blindly apply conventional clustering methods, which will not work most of the time. The main barriers are the high dimensionality, the very high feature correlation, and the (typically large) amount of noise that characterize time-series data. From these challenges, time-series clustering, as well as the associated research, can be divided into two trends:

1. The literature shows that efforts have been made to treat the high dimensional characteristic of time-series data and to develop methods of representing time-series in lower dimensions compatible with conventional clustering algorithms.
2. Many studies have focused on presenting a distance measurement based on raw time-series or the represented data.

The first step is therefore often to reduce the size of the problem. The spectrum of methods is wide. We can apply simple ones like sliding averages, business rules or more complex models like auto-encoders, Fourier transforms, PCA etc.

Once we have succeeded in reducing the dimension of the problem, the best similarity measure can be identified. One of the important challenges in clustering methods is to have a compatible and appropriate similarity measure. Literature shows that the most popular similarity measures in time-series clustering are Euclidean distance and DTW.

Finally, once we have reduced the size of the problem and found an optimal similarity distance, the question of the algorithm arises. On this point, there is almost no difference between time-series data and the context of “classic” clustering. Compared to other algorithms, partitioning algorithms are widely used because of their fast response. However, as the number of clusters needs to be pre-assigned, these algorithms are difficult to apply in most real world applications. Hierarchical clustering, on the other hand, doesn’t need the number of clusters to be pre-defined and also has a great visualization power in time-series clustering. Hierarchical clustering is a perfect tool for evaluation of dimensionality reduction or distance metrics and also has the ability to cluster time-series with unequal length, unlike partitioning algorithms. But hierarchical clustering is restricted to the small datasets because of its quadratic computational complexity.

We have also briefly discussed model-based and density-based algorithms, which are rarely used for performance and high complexity problems.

In brief, although there are opportunities for improvement in all four aspects of time-series clustering, it can be concluded that the main opportunity for future works in this field is working on new hybrid algorithms using existing clustering approaches in order to balance the quality and the expenses of clustering time-series.