Clustering de séries temporelles

Qu'est-ce qu’un clustering ?

Le clustering est une tâche d'apprentissage non supervisée visant à partitionner un ensemble de données non labellisées en groupes ou clusters homogènes. Étant dans un cadre non supervisé, nous ne possédons aucunes connaissances sur les définitions des clusters. L'objectif d'une telle tâche est de former des groupes dont les individus ont une similarité maximale avec les autres individus du groupe et une similarité minimale avec les individus des autres groupes. Il s'agit d'une approche qui peut être utilisée pour l'exploration de données, l'identification de structures dans des ensembles de données non labellisées, la synthèse de données ou comme étape de prétraitement dans un système de modélisation plus complexe.

Dans quel contexte ?

Ces dernières années, avec la puissance croissante du stockage des données et des processeurs, les applications du monde réel ont trouvé la possibilité de stocker et de conserver des données pendant de longue période. Des concepts tels que le big data, l'apprentissage automatique ou l'IA ont fait leur apparition ou se sont développés pour répondre à ces problèmes avec des données de volume exponentiel. Des changements considérables ont été apportés à la modélisation des données et le domaine des séries temporelles n'y a pas échappé. Par conséquent, lors de ces dernières années, le clustering de séries temporelles a nécessité des améliorations. Cela pour faire face à cette avalanche de données et à l'augmentation des projets et des besoins. Afin de conserver sa réputation d'outil d'exploration de données utile pour extraire des modèles et des connaissances de grands ensembles de données.

Le clustering des séries temporelles ? 

En premier temps, une série temporelle est une suite de valeurs numériques représentant l'évolution d'une quantité spécifique au cours du temps. Dans de nombreuses applications, les données sont stockées sous forme de séries temporelles, par exemple : les données météorologiques, les données de vente, les mesures biomédicales comme la pression sanguine et l'électrocardiogramme, le prix des actions, les données biométriques, etc. En conséquence, on trouve différents travaux dans des domaines variés tels que l'énergie, la finance, la bio-informatique ou la biologie.  De nombreux projets relatifs à l'analyse de séries temporelles ont été réalisés dans différents domaines à des fins diverses telles que : la correspondance de sous-séquences, la détection d'anomalies, la découverte de motifs, l'indexation, la visualisation, la segmentation, l'identification de modèles, l'analyse de tendances, la synthèse et la prévision.

Quels sont les principaux défis?

Le clustering de séries temporelles dans le contexte de grands jeux de données est un problème difficile, notamment pour deux raisons. Tout d'abord, les données de séries temporelles sont souvent de haute dimension, ce qui rend la manipulation difficile pour de nombreux algorithmes de clustering et ralentit également les processus de calculs. Ensuite, le deuxième défi concerne les mesures de similarité qui sont utilisées pour identifier les clusters. 

En examinant les travaux existants dans la littérature, on constate que le clustering de séries temporelles comporte essentiellement quatre composantes : la réduction de la dimensionnalité ou la méthode de représentation, la mesure de la distance, l'algorithme de clustering et l'évaluation de la performance.

Dans la suite de cet article, nous allons donner un aperçu des principales composantes disponibles.

A partir des séries brutes (basé sur la proximité temporelle)

Nous pouvons partir de la série brutes et appliquer directement les méthodes classiques de clustering. 

Mais attention, dans ce cas, le choix de la mesure de distance/similarité doit être soigneusement étudié. Cette question doit être traitée avant l'application de l'algorithme. On en vient à se demander ce que l'on entend par similarité entre les individus. Il est nécessaire de s'adapter aux particularités des données. 

En pratique, il est rare que l'on utilise directement les séries brutes, sauf si leur taille est faible. On effectue plutôt un traitement préalable qui permet de travailler sur une version simplifiée de la série. Nous verrons pourquoi cela est utile et parfois nécessaire dans la section suivante.

A partir d'une représentation simplifiée de la série (clustering basé sur la représentation)

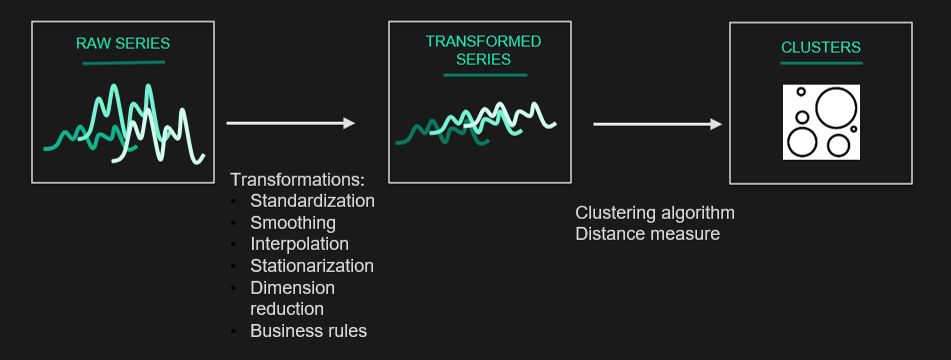
Une autre façon est de traiter les données brutes avant le clustering en appliquant des transformations simples : normalisation, lissage, interpolation, stationnarisation, etc. On peut alors produire des séries "débruitées", et c'est sur ces séries que l'on applique le clustering. 

Cette figure illustre l'importance et l'efficacité de la préparation des données :

Les mesures de similarité/distance, abordées par la suite dans l'article, peuvent alors être appliquées. Cependant le temps de calcul de certaines de ces distances peut être trop important pour les grandes bases de données, ou les performances peuvent être insuffisantes. Nous nous tournons alors vers des techniques de réduction de dimension plus complexe.

Représentation simplifiée avec réduction plus complexe de la dimension du problème

Ainsi, dans certains cas, il est souhaitable de réduire la taille des séries brutes avec des techniques plus complexes. De plus, on souhaite évidemment que ces séries réduites conservent les principales caractéristiques des séries initiales (avec une transformation qui préserve les similarités et les distances). On cherche donc un espace de dimensionnalité réduite qui permet d'extraire les principales caractéristiques des séries et de réduire leur taille.

Les raisons pour lesquelles la réduction de la dimensionnalité est très importante dans le clustering de séries temporelles est d'abord parce qu'elle réduit les besoins en mémoire. Ensuite, le calcul de la distance entre les données brutes est coûteux, et la réduction de la dimensionnalité accélère considérablement le clustering. En fait, il s'agit d'un compromis entre la vitesse et la qualité. Tous les efforts doivent être faits pour obtenir un point d'équilibre approprié.

Un exemple simple et bien connu est l'utilisation de la transformée de Fourier rapide. Toute "belle" fonction mathématique admet une décomposition en sinus et cosinus de la forme :  

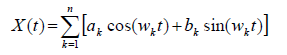
Dans cette décomposition, les coefficients a et b représentent la contribution de la fréquence ω à la série X : les basses fréquences reflètent la tendance et le cycle de la série, les fréquences saisonnières, la saisonnalité, etc. Le tableau ci-dessous présente un exemple de réduction de la dimension d'une série temporelle par transformation de Fourier. Il suffit de retenir par exemple les coefficients de Fourier les plus importants pour obtenir une représentation simplifiée de la série.

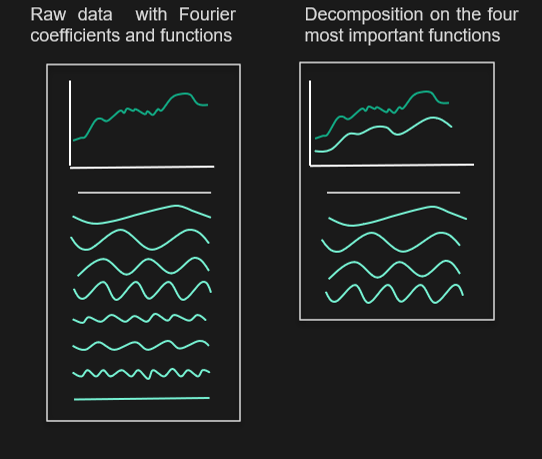
Le même principe peut être appliqué à plusieurs autres transformations :

• Fourier Transform: DFT
• Discrete Wavelet Transform: DWT
• Singular Value Decomposition via PCA : SVD
• La SSA (analyse de spectre singulier) (voir le tutoriel de modélisation de séries temporelles ) 
• Piecewise Aggregate Approximation : PAA
• Adaptive Piecewise Approximation Constante : APCA 
• Piecewise Linear Approximation : PLA
• Approximation symbolique : SAX
• Auto-encodeur 

Ici quelques exemples de telles transformations :

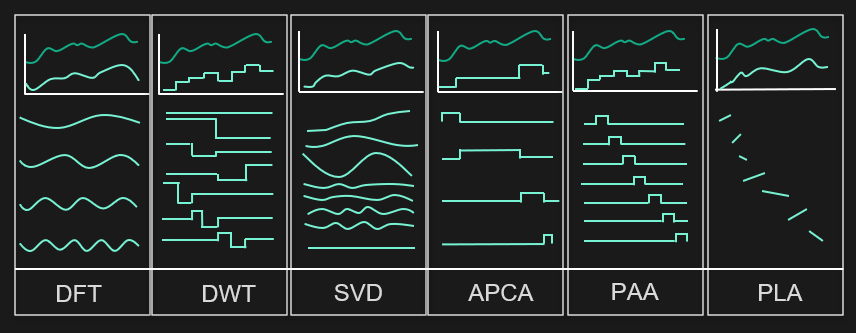
Représentation simplifiée avec des règles métiers

Une autre simplification possible consiste à appliquer des "règles métiers". En effet, selon le cas d’usage, il est possible de réduire la dimension du problème sans utiliser des méthodes statistiques complexes. Par exemple, si nous voulons effectuer un clustering sur une série temporelle représentant la consommation d'électricité sur une année avec un intervalle de 30 minutes. Il est tout à fait possible, en fonction de l'objectif, d'agréger la série (au pas horaire par exemple), ou de réduire l'historique si les motifs sont répétés, de créer des séries plus courtes (moyennes des semaines d'hiver et d'été), etc. Selon le cas, nous pouvons modifier notre jeu de données de départ et réduire la taille du problème.

Clustering basé sur des modèles

Une autre idée consiste à modéliser les séries temporelles pour capturer et résumer leur dynamique. Deux séries seront alors similaires si les modèles ajustés sont également similaires. Plusieurs idées ont été exploitées dans la littérature :

• Un modèle autorégressif, ou même ARIMA, peut être ajusté aux séries. Ces modèles sont ensuite comparés en utilisant une métrique particulière.
• Les modèles de Markov.

Cependant, en pratique, il est montré que les approches basées sur les modèles ont généralement des problèmes de scalabilité, et que leurs performances diminuent lorsque les clusters sont proches les uns des autres. Cette méthode est donc rarement utilisée.

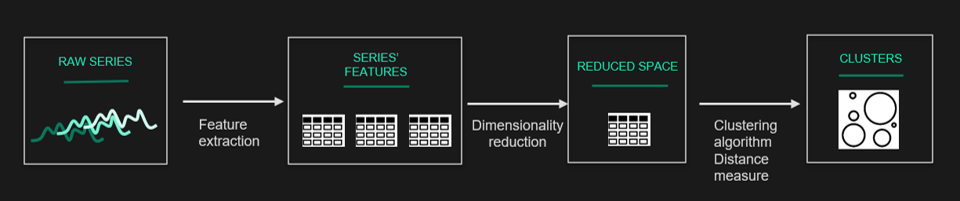
A partir de l'extraction de caractéristiques (clustering basé sur les caractéristiques)

Ici, nous poussons plus loin la logique de clustering basée sur le modèle : nous utilisons plusieurs variables qui nous permettent de qualifier les séries temporelles (tendance, saisonnalité, autocorrélation, non-linéarité, asymétrie, aplatissement, etc.) Cette extraction de caractéristiques permet la description de chaque série. 

On passe alors d'une série brute à une série de caractéristiques. Nous pouvons créer des centaines de caractéristiques pour chaque série. Il peut donc être intéressant de mettre en place un processus de sélection des variables pertinentes et/ou d'appliquer un algorithme de réduction de dimension. 

Enfin, encore une fois, nous pouvons appliquer le choix de la mesure de distance/algorithme que nous voulons en fonction des contraintes d'implémentation.

Dans le clustering de séries temporelles, les mesures de similarité/dissimilarité jouent un rôle important et ont un impact majeur sur le résultat du clustering. Cependant, le choix de la bonne mesure n'est pas une tâche évidente. Certaines mesures de similarité sont proposées sur la base d'une représentation spécifique des séries temporelles, et d'autres fonctionnent indépendamment des méthodes de représentation, ou sont compatibles avec les séries temporelles brutes. 

Normalement, lors de la réalisation d'un clustering "classique", les distances entre les individus sont basées sur la correspondance. Cependant, pour le clustering de séries temporelles, la distance peut être calculée approximativement. Il est ainsi possible de calculer la distance entre des séries dont les intervalles et la longueur d'échantillonnage sont irréguliers. Il n'est souvent pas nécessaire de chercher des mesures très exotiques, il existe des mesures de distance populaires et efficaces telles que la distance de Hausdorff (DH), la distance de Hausdorff modifiée (MODH), la distance basée sur les HMM, le Dynamic Time Warping (DTW), la distance euclidienne, la distance euclidienne dans un sous-espace PCA et la plus longue sous-séquence commune (LCSS).

Le choix de la mesure de distance dépend évidemment des objectifs, du cas d'utilisation, des caractéristiques, de la longueur et de la méthode de représentation des séries temporelles. Les recherches montrent que pour ce type de problème, nous devons faire face à des problèmes tels que le bruit, la mise à l'échelle de l'amplitude, la translation du décalage, la mise à l'échelle longitudinale, la dérive linéaire, les discontinuités et la dérive temporelle, qui sont les propriétés communes des données de séries temporelles.

Une large gamme de mesures 

Des centaines de distances ont été proposées pour classer les données, parmi lesquelles la distance euclidienne est la plus populaire. Mais, lorsqu'il s'agit de classer des séries temporelles, l'utilisation de la distance euclidienne, et de toute autre métrique de Minkowski sur des données brutes peut conduire à des résultats peu intuitifs. En particulier, cette distance est très sensible aux effets d'échelle, à la présence de points atypiques ou manquants et ne permet pas de prendre en compte les éventuels décalages temporels. En effet, des signaux très similaires peuvent par exemple être décalés dans le temps et, dans ce cas, ne pourraient pas être considérés comme proches selon la distance euclidienne standard. Pour résoudre ce problème, il existe des métriques adaptées telles que la distance DTW (Dynamic Time Warping). 

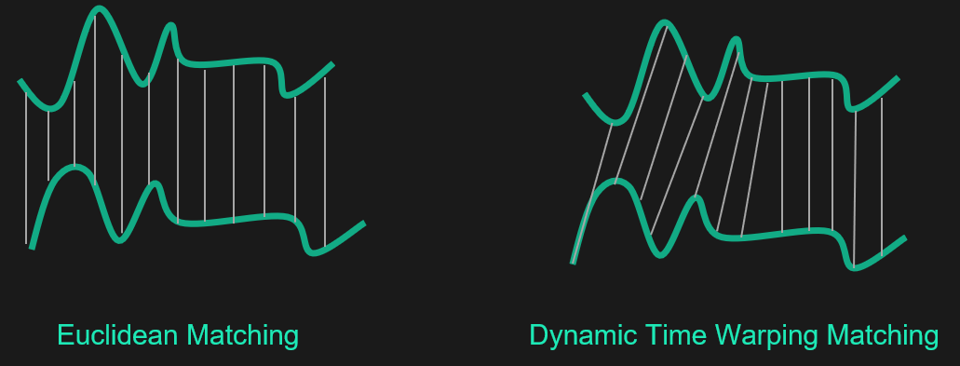
Cette distance considère un temps élastique non linéaire et explique donc les variations de la série par une déformation de l'axe du temps. Intuitivement, cela signifie que cette distance ne prend pas uniquement en compte les points alignés. Ainsi, la distance euclidienne ne prend en considération que les événements simultanés, alors que la distance DTW prend en compte les événements déphasés. Bien sûr, il ne s'agit pas d'une mesure magique qui fonctionne dans tous les cas. Il existe de nombreuses autres métriques, et il se peut que la distance euclidienne reste un bon choix.  Il n'existe pas de métrique ou d'algorithme de clustering dont on puisse dire qu'il surpasse tous les autres. Tout dépend du contexte de l'application. Il faut donc expérimenter différentes alternatives et sélectionner la meilleure. 

En fonction de l'objectif et de la longueur des séries temporelles, les quatre méthodes mentionnées ci-dessus peuvent être testées : à partir de la série temporelle, d'une représentation simplifiée de la série, du clustering basé sur un modèle, ou de l'extraction de caractéristiques. En fonction de la méthode et de la volonté de former des clusters similaires dans le temps ou dans la forme, il existe dans la littérature de nombreuses autres mesures, par exemple : 

• Les mesures de similarité basée sur la proximité temporelle qui permet de trouver les séries temporelles similaires en termes de temps et de forme comme :  Euclidean, DTW, LCSS, etc. 
• Les mesures de similarité basée sur la compression : appropriée pour les séries temporelles courtes et longues comme CDM, Autocorrélation, Short time- series distance, Pearson's correlation coefficient, Cepstrum, Piecewise normalization and Cosine wavelets.
• Les mesures de similarité basée sur les caractéristiques : appropriée pour les longues séries temporelles telles que les statistiques, les coefficients, etc. 
• Les mesures de similarité basée sur un modèle tel que ARMA

Discussion sur les mesures de distance  

Il existe de nombreuses mesures de distance proposées par les chercheurs et le choix d'une mesure de distance suffisamment précise est controversé dans le domaine du clustering de séries temporelles. Cependant, la conclusion suivante peut être tirée :

• Un compromis entre la vitesse et la précision doit être trouvé dans l'utilisation des métriques. 
• Un grand défi est la question de l'incompatibilité de la mesure de distance avec la méthode de représentation. Par exemple, l'une des approches courantes appliquées à l'analyse des séries temporelles est basée sur le domaine fréquentiel. En utilisant cet espace, il est difficile de trouver la similarité entre les séquences.
• La distance euclidienne et le DTW sont les méthodes les plus courantes pour mesurer la similarité dans le clustering des séries temporelles. Les recherches ont montré qu'en termes de précision, la distance euclidienne est étonnamment compétitive, mais que la méthode DTW a aussi des points forts qui ne peuvent être déclinés.

En règle générale, le clustering peut être classé en cinq groupes : les algorithmes de clustering hiérarchique, de partitionnement, basés sur un modèle, basés sur la densité et hybrides. Dans ce qui suit, l'application de chaque méthode est discutée.

Clustering hiérarchique

Également appelé Hierarchical cluster analysis or HCA, est un algorithme de clustering non supervisé, il est l'une des techniques de clustering les plus populaires et faciles à comprendre. Cet algorithme est divisé en deux types :

1. Le clustering hiérarchique agglomératif : il considère chaque élément comme un cluster, puis fusionne progressivement les clusters (bottom-up).
2. Le clustering hiérarchique divisé : commence avec tous les objets comme un seul cluster, puis divise le cluster pour atteindre les clusters avec un seul objet (top-down).

En général, les algorithmes hiérarchiques sont faibles en termes de qualité car ils ne peuvent pas ajuster les clusters après la division d'un cluster dans la méthode de division, ou après la fusion dans la méthode d'agglomération. Par conséquent, les algorithmes de clustering hiérarchique sont généralement combinés avec un autre algorithme en tant qu'approche de clustering hybride pour remédier à ce problème. 

Sans entrer dans les détails de l'algorithme, il génère une matrice de distance par paire de séries temporelles. Mais pour générer cette matrice, et plus particulièrement pour calculer les distances/similarités entre les séries, il est nécessaire de choisir une mesure de distance/similarité. On reconnaît ici l'importance du choix de cette distance qui va conditionner les résultats de l'algorithme. De plus, grâce à cette matrice de distance, le clustering hiérarchique a un grand pouvoir de visualisation ce qui en fait une approche intéressante à utiliser pour le clustering de séries temporelles dans une large mesure.

En outre, l'une des grandes forces de cet algorithme est le fait qu'il n'a pas besoin du nombre de clusters recherchés comme paramètre d'entrée. C'est une caractéristique remarquable car il peut être très difficile de trouver ce paramètre, parfois nécessaire pour certains algorithmes comme nous le verrons par la suite.

De plus, contrairement à de nombreux algorithmes, le clustering hiérarchique a la capacité de regrouper des séries temporelles de longueur inégale. Il est possible de regrouper ces séries à l'aide d’une mesure de distance élastique appropriée, comme le Dynamic Time Warping (DTW) ou le Longest Common Sub-sequence (LCSS), qui sont utilisées pour calculer la dissimilarité/similarité des séries temporelles. Cependant, le clustering hiérarchique n'est pas capable de traiter efficacement de grandes séries temporelles en raison de sa complexité de calcul quadratique et, par conséquent, il est limité à de petits ensembles de données en raison de sa faible scalabilité.

Outre le choix de l'algorithme et de la mesure de distance, il est nécessaire de choisir le critère d'agrégation. Dans l’algorithme hiérarchique, nous serons amenés à considérer la distance entre des groupes d'individus et la question suivante se posera : comment calculer la distance en présence de groupes ? Différentes possibilités existent. 

Tout d'abord, trois critères qui fonctionnent quelle que soit la mesure de distance ou de dissimilarité (parmi beaucoup d'autres) : 

• Le critère de liaison minimale (ou liaison simple), qui se base sur les deux éléments les plus proches ; 
• Le critère de liaison maximale (ou liaison complète), qui se base sur les deux éléments les plus éloignés ; 
• Le critère de liaison moyenne, qui va utiliser la moyenne des distances entre les éléments de chaque classe pour effectuer les regroupements. 

Ensuite, dans le cadre de la distance euclidienne, d'autres critères peuvent être utilisés. Le plus couramment utilisé est le critère de Ward, qui est basé sur l'augmentation de l'inertie. Sans entrer dans les détails, ce critère revient à agréger deux classes de manière à ce que l'augmentation de l'inertie intra-classe soit la plus faible possible, afin que les classes restent les plus homogènes possibles.   

En fonction du critère choisi, on peut se retrouver avec des arbres aux formes très différentes. Au final, il est important de se rappeler qu'il n'existe pas une seule bonne méthode, tout comme il n'existe pas une seule méthode de clustering. Il est recommandé de tester plusieurs approches et d'analyser les résultats.

Clustering par partitionnement 

L'objectif du clustering non-hiérarchique est le même que celui du clustering hiérarchique, mais cette fois, le nombre de clusters doit être pré-attribué. Pour une mesure de distance donnée et pour un nombre connu de classes k. Il est facile d'imaginer une solution de classification simple et optimale : énumérer toutes les possibilités de clustering imaginables et garder la meilleure. Cependant, cette solution n'est pas applicable en pratique, car le nombre de combinaisons possibles de clusters devient très vite énorme. Mais des solutions approximatives peuvent être obtenues grâce à des heuristiques, et des algorithmes. Leur principe fondamental est contenu dans la méthode des centres mobiles. 

L'idée principale est la minimisation de la distance totale (typiquement la distance euclidienne) entre tous les objets d'un cluster et leur centre du cluster.

L'algorithme ne conduit pas nécessairement à un optimum global : le résultat final dépend des centres initiaux. En pratique, nous l'exécutons plusieurs fois (avec des centres initiaux différents). Ensuite, soit on garde la meilleure solution, soit on cherche des regroupements stables pour identifier les individus qui appartiennent aux mêmes groupes. 

Les variantes les plus connues des centres mobiles sont (parmi beaucoup d'autres) : 

• La méthode K-means
• Les méthodes de clustering dynamique
• Les méthodes K-medoids

Dans ces algorithmes de clustering, le nombre de clusters, k, doit être pré-assigné, ce qui est une tâche très compliquée pour de nombreuses applications. C'est encore plus compliqué avec les données de séries temporelles car les ensembles de données sont très grands et les contrôles de diagnostic pour déterminer le nombre de clusters ne sont pas faciles. 

Cependant, ces algorithmes sont très rapides par rapport au clustering hiérarchique, ce qui les rend très adaptés au clustering de séries temporelles et donc utilisé dans de nombreux travaux. Les clusters peuvent être construits de manière "hard" ou "soft", ce qui signifie que soit un objet est assigné à un cluster (hard), soit on lui assigne une probabilité d'être dans un cluster (soft).

Clustering basé sur les modèles  

Le clustering basé sur un modèle suppose que les données ont été générées par un modèle et tente de récupérer le modèle original à partir des données. Dans la littérature, il y a assez peu de publications de recherche qui montrent l'utilisation de ces méthodes. La plupart du temps, ils construisent leur clustering à l'aide de modèles polynomiaux, de modèles mixtes gaussiens, d'ARIMA, de chaînes de Markov ou de réseaux neuronaux. En général, le clustering basé sur un modèle présente deux inconvénients : d'abord,les grands ensembles de données sont lents à traiter . Deuxièmement, et c'est le plus important, il faut définir des paramètres basés sur les hypothèses de l'utilisateur qui peuvent être fausses et, par conséquent, les clusters obtenus seraient inexacts.

Cette méthode ne sera pas plus abordée car elle n'est presque jamais utilisée dans la pratique.

Clustering basé sur la densité

Le clustering basé sur la densité fait référence à des méthodes d'apprentissage non supervisées qui identifient des groupes/clusters distincts dans les données en se basant sur l'idée qu'un cluster dans un espace de données est une région contiguë de haute densité ponctuelle, séparée d'autres clusters par des régions contiguës de basse densité ponctuelle. L'un des algorithmes les plus connus qui fonctionne selon le concept de densité est DBSCAN. 

Cependant, en examinant la littérature, on remarque que le clustering basé sur la densité n'a pas été largement utilisé pour le clustering de données de séries temporelles en raison de sa complexité plutôt élevée.

Approche hybride 

Nous avons présenté les approches séparément. En revanche, dans la pratique, il peut être utile de les utiliser ensemble. En mélangeant les approches, on peut profiter de leurs principaux avantages, à savoir :

• La possibilité d'analyser un grand nombre d'individus, ce qui est le point fort des méthodes non hiérarchiques (pour un certain nombre d'observations, il devient difficile d'appliquer directement les méthodes hiérarchiques) ; 
• Le choix d'un nombre optimal de classes, rendu possible par la classification hiérarchique. 

En pratique, dès que le jeu de données devient important, il est recommandé de mettre en œuvre une approche hybride pour avoir le meilleur compromis entre performance et rapidité d'exécution.

L'évaluation correcte de la performance d'un clustering est toujours un problème ouvert, et pas seulement pour le clustering de séries temporelles. Comme il s'agit d'un problème non supervisé, nous n'avons pas de label pour établir des mesures de performance. La définition d'un bon clustering dépend du problème et est souvent subjective. Par exemple, le nombre de clusters, la taille des clusters, la définition des valeurs aberrantes, et la définition de la similarité entre les séries temporelles d'un problème sont tous des concepts qui dépendent de la tâche à accomplir et doivent être déclarés subjectivement. 

L'évaluation du clustering de séries temporelles devrait suivre certaines recommandations : 

• Le biais de mise en œuvre doit être évité par une conception minutieuse des expériences. 
• Les nouvelles méthodes de mesures de similarité doivent être comparées à des mesures simples et stables telles que la distance euclidienne.

Le résultat peut être évalué à l'aide de certaines mesures. La visualisation et les mesures scalaires sont les principales techniques d'évaluation de la qualité du clustering.

Les fonctions objectives typiques du clustering formalisent le but d'atteindre une similarité intra-classe élevée (les objets au sein d'une classe sont similaires) et une similarité inter-classe faible (les objets de différentes classes sont dissemblables).  Les indices de validité interne évaluent les résultats du clustering en utilisant uniquement les caractéristiques et les informations inhérentes à un jeu de données. Ils sont généralement utilisés dans le cas où les vraies solutions (vérité terrain) sont inconnues. 

Les clusters peuvent être interprétés en utilisant par exemple des outils statistiques communs tels que les moyennes, les écarts types, les min/max, etc. Il existe également de nombreux indices internes tels que la somme des carrés de l'erreur, l'indice Silhouette, l'indice Davies-Bouldin, Calinski-Harabasz, Dunn, l'indice R-carré, l'indice Hubert-Levin (indice C), l'indice Krzanowski-Lai, l'indice Hartigan, l'indice RMSSTD (Root-Mean-Square Standard Deviation), l'indice SPR (Semi-Partial R-squared), l'indice CD (Distance between two clusters), l'indice inter-intra pondéré, l'indice d'homogénéité et l'indice de séparation. La somme des erreurs quadratiques (SSE) est une fonction objective qui décrit la cohérence d'un cluster donné. Les "meilleurs" clusters devraient donner des valeurs SSE plus faibles. Pour évaluer les clusters en termes de performances, la somme des erreurs quadratiques (SSE) peut être considérée comme la mesure la plus courante dans les travaux existants. Pour chaque série temporelle, l'erreur est la distance au cluster le plus proche.

Cependant, dans le contexte du clustering, la vision business est souvent très importante pour considérer ce qu'est un bon clustering et une bonne performance ! Il peut y avoir des résultats impossibles à obtenir, d’autres nous ne voulons pas, des attentes particulières, un nombre de clusters à respecter, etc.

Les caractéristiques intrinsèques des données, les séries temporelles, font de l'exercice du clustering un véritable défi. En effet, il est difficile d'appliquer aveuglément les méthodes de clustering conventionnelles, qui ne fonctionnent pas la plupart du temps. Les principaux obstacles sont la haute dimensionnalité, la corrélation très élevée des caractéristiques et la quantité généralement importante de bruit qui caractérisent les données de séries temporelles. A partir de ces défis, le clustering de séries temporelles, ainsi que la recherche associée, peuvent être divisés en deux : 

1. La littérature montre que de nombreux efforts ont été faits sur la caractéristique de haute dimension des données de séries temporelles et ont essayé de présenter une façon de représenter les séries temporelles dans une dimension inférieure compatible avec les algorithmes de clustering conventionnels.
2. Un grand nombre de recherches se sont concentrées sur la présentation d'une mesure de distance basée sur les séries temporelles brutes ou les données transformées.

La première étape consiste donc souvent à réduire la dimension du problème. Le spectre des méthodes est large. Nous pouvons appliquer des méthodes simples comme les moyennes glissantes, les règles métiers ou des modèles plus complexes comme les auto-encodeurs, les transformées de Fourier, l'ACP, etc. 

Une fois que nous avons réussi à réduire la dimension du problème. La meilleure mesure de similarité peut être recherchée. L'un des défis importants des méthodes de clustering est de disposer d'une mesure de similarité compatible et appropriée. Finalement, la littérature montre que les mesures de similarité les plus populaires dans le clustering de séries temporelles sont la distance euclidienne et DTW.

Enfin, une fois que nous nous sommes attachés à réduire la taille du problème et à trouver une distance de similarité optimale, la question de l'algorithme se pose. Sur ce point, il n'y a presque aucune différence avec un clustering "classique". Par rapport aux autres algorithmes, les algorithmes de partitionnement sont largement utilisés en raison de leur rapidité de réponse. Cependant, comme le nombre de clusters doit être attribué à l'avance, ces algorithmes sont difficiles à appliquer dans la plupart des applications du monde réel. Le clustering hiérarchique, quant à lui, n'a pas besoin que le nombre de clusters soit prédéfini et possède également un grand pouvoir de visualisation dans le clustering de séries temporelles. C'est un outil parfait pour l'évaluation de la réduction de la dimensionnalité ou des métriques de distance. Et il possède la capacité de regrouper des séries temporelles de longueur inégale qui est un autre atout par rapport aux algorithmes de partitionnement. Mais le clustering hiérarchique est limité aux petits ensembles de données en raison de sa complexité de calcul quadratique. 

Nous avons également abordé brièvement les algorithmes basés sur le modèle et sur la densité, qui sont rarement utilisés pour des problèmes de performance et de haute complexité. 

En bref, bien qu'il existe des possibilités d'amélioration dans les quatre aspects du clustering de séries temporelles, on peut conclure que la principale opportunité pour les travaux futurs dans ce domaine pourrait être de travailler sur de nouveaux algorithmes hybrides en utilisant les approches de clustering existantes afin d'équilibrer la qualité et les coûts du clustering de séries temporelles.